I put together a presentation going through the proof of the noisy-channel coding theorem (based on the proofs given in Cover and Thomas 2006, Ch.7 and MacKay 2003, Ch.10), a central result in information theory, which is a statement about noisy channels (a set up where a message passed from sender to receiver is disturbed by some random process during transmission).

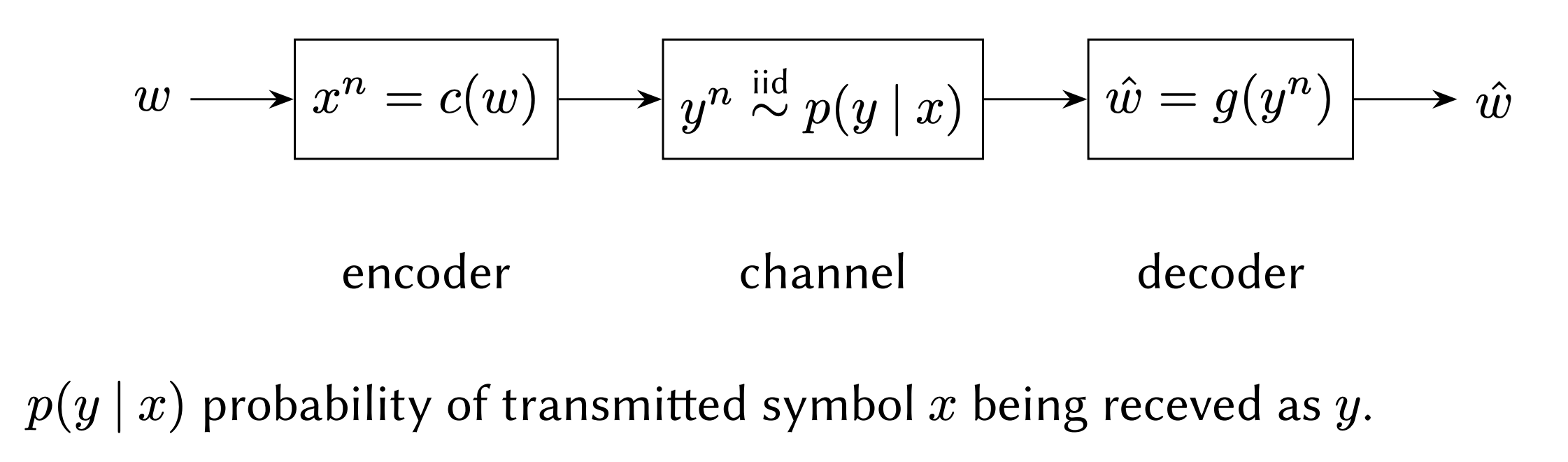
The theorem says that it’s possible to communicate across such a channel with arbitrarily low probability of error, at any rate of transmission bounded by the mutual information between encoded sequences and received sequences, as long as the length of the code is allowed to be as long as necessary.

Slides here.